Risk Management Introduction
See also: Introduction to risk analysis, Planning a risk analysis, The quality of a risk analysis
The Risk Management approach
Risk management is the process of identifying risk issues and the options for controlling them, commissioning a risk assessment, reviewing the results and selecting amongst the assessed options to best meet the goals.
The following flowchart shows the various aspects of the risk management approach:
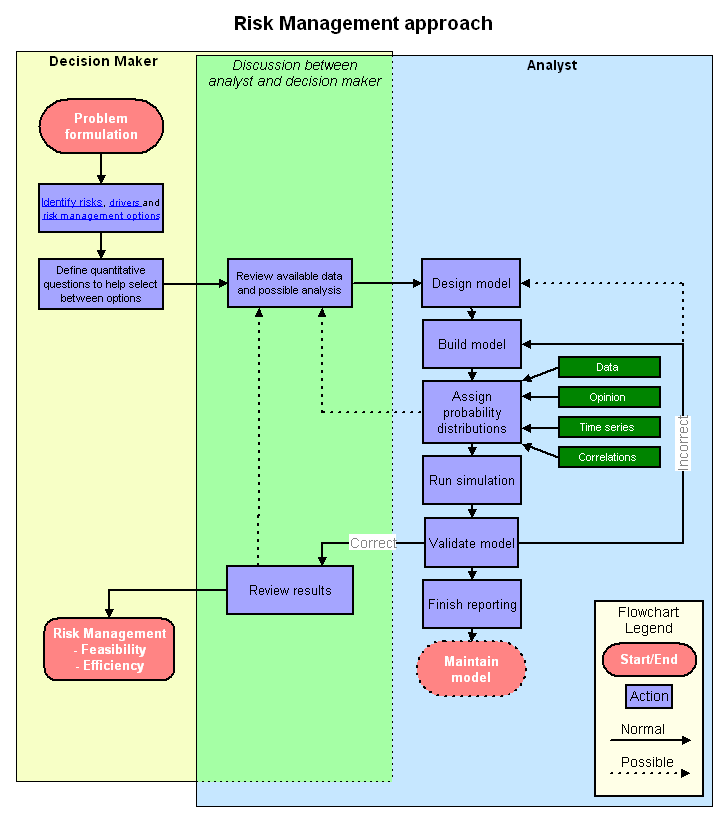
The purpose of risk analysis is to help managers better understand the risks (and opportunities) they face and to evaluate the options available for their control. In general, risk management options can be divided into several groups:
Acceptance (do nothing)
Nothing is done to control the risk or one's exposure to that risk. Appropriate for risks where the cost of control is out of proportion with the risk. It is usually appropriate for low probability, low impact risks and opportunities of which one normally has a vast list, but you may be missing some high value risk mitigation or avoidance options, especially where they control several risks at once. If the chosen response is acceptance, some considerable thought should be given to risk contingency planning.
Increase
You may find that you are already spending considerable resources to manage a risk that is excessive compared to the level of protection that it affords you. In such cases, it is logical to reduce the level of protection and allocate the resources to manage other risks, thereby achieving a superior overall risk efficiency. Examples are:
- Remove a costly safety regulation for nuclear power plants that affects a risk that would otherwise still be miniscule;
- Cease requirement to test all slaughtered cows for BSE and use saved money for hospital upgrades.
It may be logical, but nonetheless politically unacceptable. There are not too many politicians or CEO's who want to explain to the public that they've just authorised less caution in handling a risk.
Get more information
A risk analysis can describe the level of uncertainty there is about the decision problem (here we use uncertainty as distinct from inherent randomness). Uncertainty can often be reduced by acquiring more information (whereas randomness cannot). Thus, a decision-maker can determine that there is too much uncertainty to make a robust decision and request that more information be collected. Using a risk analysis model, the risk analyst can advise the least cost method of collecting extra data that would be needed to achieve the required level of precision. Value-of-information arguments (see Section 5.4.6) can be used to assess how much, if any, extra information should be collected.
Avoidance (elimination)
This involves changing a method of operation, a project plan, an investment strategy, etc. so that the identified risk is no longer relevant. Avoidance is usually employed for high probability, high impact type risks. Example are:
- Use a tried and tested technology instead of the new one that was originally envisaged;
- Change country location of a factory to avoid political instability;
- Scrap the project altogether
Note that there may be a very real chance of introducing new (and perhaps much more important) risks by changing your plans.
Reduction (mitigation)
Reduction involves a range of techniques, which may be used together, to reduce the probability of the risk, its impact, or both. Examples are:
- Build in redundancy (standby equipment, back-up computer at different location);
- Perform more quality tests or inspections;
- Provide better training to personnel;
- Spread risk over several areas (portfolio effect);
Reduction strategies are used for any level of risk where the remaining risk is not of very high severity (very high probability and impact) and where the benefits (amount risk is reduced by) outweigh the reduction costs.
Contingency planning
These are plans devised to optimise the response to risks should they occur. They can be used in conjunction with acceptance and reduction strategies. A contingency plan should identify individuals who take responsibility for monitoring the occurrence of the risk, and/or identified risk drivers for changes in the risk's probability or possible impact. The plan should identify what to do, who should do it and in which order, the window of opportunity, etc. Examples are:
- Have a trained firefighting team on-site;
- Have a pre-prepared press release;
- Have a phone list visible (or email distribution list) of whom to contact if the risk occurs;
- Reduce police and emergency service leave during a strike;
- Fit lifeboats on ships.
Risk Reserve
Management's response to an identified risk is to add some reserve (buffer) to cover the risk should it occur. Appropriate for small to medium impact risks. Examples are:
- Allocate extra funds to a project;
- Allocate extra time to complete a project;
- Have cash reserves;
- Have extra stock in shop for a holiday weekend;
- Stockpile medical and food supplies
Insurance
Essentially, this is a risk reduction strategy, but it is so common that it is worth mentioning separately. If an insurance company has done its numbers correctly, in a competitive market you will pay a little above the expected cost of the risk (i.e. probability * expected impact should the risk occur). In general, we therefore insure for risks that have an impact outside our comfort zone, (i.e. where we value the risk higher than its expected value). Alternatively, you may feel that your exposure is higher than the average policy purchaser in which case insurance may be under your expected cost and therefore extremely attractive
Risk transfer
This involves manipulating the problem so that the risk is transferred from one party to another. A common method of transferring risk is through contracts, where some form of penalty is included into a contractor's performance. The idea is appealing used often but can be very inefficient. Examples are:
- Penalty clause for running over agreed schedule;
- Performance guarantee of product;
- Lease a maintained building from the builder instead of purchasing; and
- Purchase an advertising campaign from some media body or advertising agency with payment contingent on some agreed measure of success
You can also consider transferring risks to you, where there is some advantage to relieving another party of a risk. For example, if you can guarantee a second party against some small risk resultant from an activity you wish to take that provides you with much greater benefit than the other party's risk, the second party may remove its objection to your proposed activity.
Evaluating risk management options
The manager evaluating the possible options for dealing with a defined risk issue needs to consider many things:
- How sensitive is the ranking of each option to model uncertainties?;
- What are the benefits relative to the costs associated with each risk management option?;
- Are there any secondary risks associated with a chosen risk management option?; and
- How practical will it be to execute the risk management option?
- Is the risk assessment of sufficient quality to be relied upon?
- How sensitive is the ranking of each option to model uncertainties?
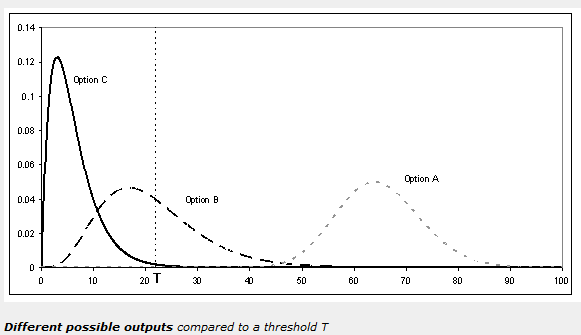 On this last point,
we almost always would like to have better data, or greater certainty
about the form of the problem: we would like the distribution of what
will happen in the future to be as narrow as possible. However, a decision-maker
cannot wait indefinitely for better data and, from a decision-analytic
point of view, may quickly reach the point where the best option has been
determined and no further data (or perhaps only a very dramatic change
in knowledge of the problem) will make another option preferable. This
concept is known as decision-sensitivity. For example, in the figure on
the right, the decision-maker considers any output below a threshold T
(shown with a dashed line) to be perfectly acceptable (perhaps this is
a regulatory threshold or a budget). The decision-maker would consider
option A to be completely unacceptable, option C to be perfectly fine,
and would only need more information about option B to be sure whether
it was acceptable or not, despite all three having considerable uncertainty.
On this last point,
we almost always would like to have better data, or greater certainty
about the form of the problem: we would like the distribution of what
will happen in the future to be as narrow as possible. However, a decision-maker
cannot wait indefinitely for better data and, from a decision-analytic
point of view, may quickly reach the point where the best option has been
determined and no further data (or perhaps only a very dramatic change
in knowledge of the problem) will make another option preferable. This
concept is known as decision-sensitivity. For example, in the figure on
the right, the decision-maker considers any output below a threshold T
(shown with a dashed line) to be perfectly acceptable (perhaps this is
a regulatory threshold or a budget). The decision-maker would consider
option A to be completely unacceptable, option C to be perfectly fine,
and would only need more information about option B to be sure whether
it was acceptable or not, despite all three having considerable uncertainty.
Inefficiencies in transferring risks to others
A common method of managing risks is to force or persuade another party to accept the risk on your behalf. For example, an oil company could require that a sub-contractor welding a pipeline accepts the costs to the oil company resulting from any delays they incur or any poor workmanship. The welding company will, in all likelihood, be far smaller than the oil company, so possible penalty payments would be catastrophic. The welding company will therefore value the risk as very high and will require a premium greatly in excess of the expected value of the risk. On the other hand, the oil company may be able to absorb the risk impact relatively easily, so would not value the risk as highly. The difference in the utility of these two companies is shown in the figures below, which demonstrates that the oil company will pay an excessive amount to eliminate the risk.
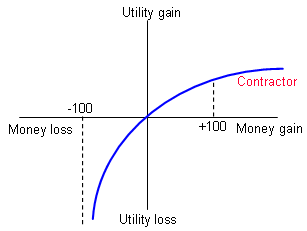
In the figure above the contractor's utility function is highly concave over the money gain/loss range in question. That means, for example, that the contractor would value a loss of 100 units of money (eg. $100,000) as a vastly larger loss in utility terms than a gain of $100,000 might be.
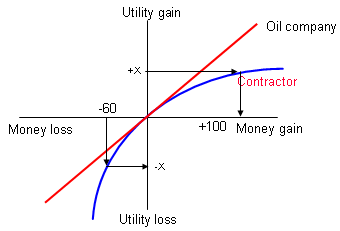
Over that same money gain/loss range, the oil company has an almost exactly linear utility function. The contractor, required to take on a risk with an expected value of -$60,000, would value this as -X utiles. To compensate, the contractor would have to charge an additional amount well in excess of $100,000. The oil company, on the other hand, would value -$60,000 in rough balance with +$60,000, so will be paying considerably in excess of it's valuation of the risk to transfer it to the contractor.
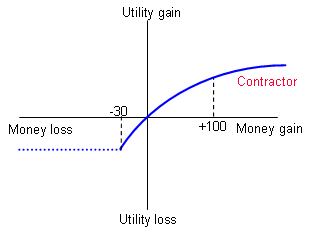
Imagine the risk has a 10% probability of occurring, and its impact would be -$300,000, to give an expected value of -$30,000. If $300,000 is the total capital value of the contractor, it won't much matter to the contractor whether the risk impact is $300,000 or $3,000,000 - they still go bust. This is shown by the shortened utility curve and the horizontal dashed line for the contractor.
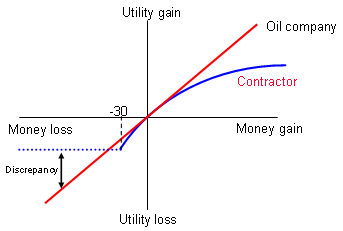
In this situation, the contractor now values any risk with an impact that exceeds its capital value at a level that is less than the oil company (shown as 'Discrepancy'). It may mean that the contractor can offer a more competitive bid than another, larger contractor who would feel the full risk impact, but the oil company will not have covered the risk it had hoped to transfer, and so again will be paying more than it should to offload the risk. Of course, one way to avoid this problem is to require evidence from the contractor that they have the necessary insurance or capital base, to cover the risk it is being asked to absorb.
A far more realistic approach to sharing risks is through a partnership arrangement. A list of risks that may impact on various parties involved in the project is drawn up and one then asks for each risk:
- How big is the risk?
- What are the risk drivers?
- Who is in control of the risk drivers? Who has the experience to control them?
- Who could absorb the risk impacts?
- How can we work together to manage the risks?
- What arrangement would efficiently allocate the risk impacts and rewards for good risk management?
- Can we insure, etc. to share risks with outsiders?
The more one can allocate ownership of risks, and opportunities, to those who control them the better - up to the point where the owner could not reasonably bear the risk impact where others can. Answering the questions above will help you construct a contractual arrangement that is risk efficient, workable and tolerable to all parties.
Risk registers
A risk register is a document or database that lists each risk pertaining to a project or organization, along with a variety of information that is useful for the management of those risks. The risks listed in a risk register will have come from some collective exercise to identify risks. The following items are essential in any risk register entry:
- Date the register was last modified
- Name of risk
- Description of what the risk is
- Description of why it would occur
- Description of factors that would increase or decrease its probability of occurrence or size of impact (risk drivers)
- Semi-quantitative estimates of its probability and potential impact
- P-I scores
- Name of owner of the risk (that person who will assume responsibility for monitoring the risk and effecting any risk reduction strategies that have been agreed)
- Details of risk reduction strategies that it is agreed will be taken (i.e. strategy that will reduce the impact on the project should the risk event occur and/or the probability of its occurrence)
- Reduced impact and/or probability of the risk given the above agreed risk reduction strategies have been taken
- Ranking of risk by scores of the reduced P-I
- Cross-referencing the risk event to identification numbers of tasks in a project plan or areas of operation or regulation where the risk may impact
- Description of secondary risks that may arise as a result of adopting the risk reduction strategies
- Action window - the period during which risk reduction strategies must be put in place
- Description of other optional risk reduction strategies
- Ranking of risks by the possible effectiveness of further risk mitigation [effectiveness = (total decrease in risk)/(cost of risk mitigation action)]
- Fall back plan in the event the risk event still occurs
- Name of person who first identified risk
- Date risk was first identified
- Date risk was removed from list of active risks (if appropriate)
A risk register should include a description of the scale used in the semi-quantitative analysis, as explained in the section on P-I scores. A risk register should also have a summary that lists the top risks (ten is a fairly usual number but will vary according to the project or overview level). The 'top' risks are those that have the highest combination of probability and impact (i.e. severity), after the reducing effects of any agreed risk reduction strategies have been included.
Risk registers lend themselves perfectly to being stored in a networked database. In this way, risks from each project or regulatory body's concerns, for example, can be added to a common database. Then, a project manager can access that database to look at all risks to his or her project. The finance director, lawyer, etc. can look at all the risks from any project being managed by their departments and the chief executive can look at the major risks to the organization as a whole. What is more, head office has an easy means for assessing the threat posed by a risk that may impact on several projects or areas at the same time. 'Dashboard' software can bring the outputs of a risk register into appropriate focus for the decision-makers.
P-I tables
The risk identification stage attempts to identify all risks, each of which threatens the achievement of the project's or organization's goals. It is clearly important, however, that attention is focused on those risks that pose the greatest threat.
Defining qualitative risk descriptions
A qualitative assessment of the probability P of a risk event (a possible event that would produce a negative impact on the project or organization) and the impact(s) it would produce I can be made by assigning descriptions to the magnitudes of these probabilities and impacts. The assessor is asked to describe the probability and impact of each risk, selecting from a predetermined set of phrases like: Nil, Very Low, Low, Medium, High and Very High. A range of values is assigned to each phrase in order to maintain consistency between the estimates of each risk. An example of the value range that might be given to each phrase in a risk register for a particular project is shown in this table:
|
Category |
Probability |
Delay |
Cost $k |
Quality |
|
Very high |
10-50% |
>100 days |
>1000 |
Failure to meet acceptance criteria |
|
High |
5-10% |
30-100 days |
30-100 |
Failure to meet > 1 important specification |
|
Medium |
2-5% |
10-30 days |
100-300 |
Failure to meet an important specification |
|
Low |
1-2% |
2-10 days |
20-100 |
Failure to meet > 1 minor specification |
|
Very low |
<1% |
< 2 days |
<20 |
Failure to meet a minor specification |
Note that the value ranges are not evenly spaced. Ideally there is a multiple difference between each range (in this case roughly 3). If the same multiple is applied for probability and impact scales we can more easily determine severity scores as described below. The value's range can be selected to match the size of the project. Alternatively, they can be matched to the effect the risks would have on the organization as a whole. The drawback in making the definition of each phrase specific to a project is that it becomes very difficult to perform a combined analysis of the risks from all projects that the organization is involved in. From a corporate perspective one can describe how a risk affects the health of a company, as shown in this table:
|
Category |
Description |
|
Catastrophic |
Jeopardizes the existence of the company |
|
Major |
No longer possible to achieve business objectives. |
|
Moderate |
Reduced ability to achieve business objectives. |
|
Minor |
Some business disruptions but little affect on business objectives |
|
Insignificant |
No impact on business strategy objectives. |
Visualising a portfolio of risks
A P-I table offers a quick way to visualize the relative riskiness of all identified risks that pertain to a project (or organization). The table below illustrates an example. All risks are plotted on the one table, allowing for the easy identification of the most threatening risks as well as providing a general picture of the overall riskiness of the project. Risks number 13, 2, 12 and 15 are the most threatening in this example.

The impact of a project risk that is most commonly considered is a delay in the scheduled completion of the project. However, an analysis may also consider the increased cost of the project resulting from each risk. It might further consider other, less numerically definable impacts on the project, for example: the quality of the final product; the goodwill that could be lost; sociological impacts; political damage or strategic importance of the project to the organization. A P-I table can be constructed for each type of impact, enabling the decision-maker to gain a more rounded understanding of a project's riskiness.
P-I tables can be constructed for the various types of impact of each single risk. The next table illustrates an example, where the schedule delay (T), cost ($) and product quality (Q) impacts are shown for a specific risk. The probability of each impact may not be the same. In this example, the probability of the risk event occurring is high and hence the probability of schedule delay and cost impacts are high, but it is considered that, even if this risk event does occur, the probability of a quality impact is still low. In other words, there is a fairly small probability of a quality impact even when the risk event does occur.

Ranking risks
P-I scores can be used to rank the identified risks. A scaling factor, or weighting, is assigned to each phrase used to describe each type of impact. The following table provides an example of the type of scaling factors that could be associated with each phrase/impact type combination:
|
Category |
Score |
|
Very high |
5 |
|
High |
4 |
|
Medium |
3 |
|
Low |
2 |
|
Very low |
1 |
In this type of scoring system. the higher the score the greater the risk. In Table 4 the categories were determined by using a rough multiplier. A base measure of risk is Probability * Impact. The scoring system of the table above is on a log scale, so to be consistent we can define the severity of a risk with a single type of impact as:
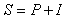
Which leaves the severity on a log scale too. If a risk has k possible types of impact (quality, delay, cost, reputation, environmental, etc) perhaps with different probabilities for each impact type, we can still combine them into one score as follows:
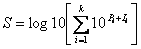
The severity scores are then used to determine the most important risks, enabling the management to focus resources on reducing or eliminating risks from the project in a rational and efficient manner. A drawback to this approach of ranking risks is that the process is quite dependent on the granularity of the scaling factors that are assigned to each phrase describing the risk impacts. If we have better information on probability or impact than the scoring system would allow, we can assign a more accurate (non integer) score.
In the scoring regime of the discussed table, for example, a high severe risk could be defined as having a score higher than 7, a low risk as having a score lower than 5. Given the crude scaling used, risks with a severity of 7 may requite further investigation to determine whether they should be categorised as high severity. This table shows how this segregates the risks shown in a P-I table into the three regions:
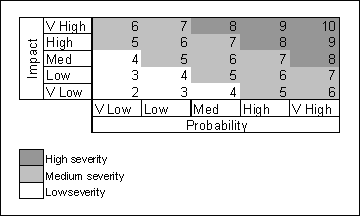
P-I scores for a project provide a consistent measure of risk that can be used to define metrics and perform trend analyses. For example, the distribution of severity scores for a project gives an indication of the overall 'amount' of risk exposure. More complex metrics can be derived using severity scores, allowing risk exposure to be normalized and compared with a baseline status. These permit trends in risk exposure to be identified and monitored, giving valuable information to those responsible for controlling the project.
Efficient risk management with severity scores
Efficient risk management seeks to achieve the maximum reduction in risk for a given amount of investment (of people, time, money, restriction of liberty, etc.). Thus, we need to evaluate in some sense the ratio (reduction in risk)/(investment to achieve reduction). If you use the log scale for severity described here, this would equate to calculating:
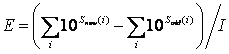
where E stands for Efficiency and I for Investment. Whatever risk management options provide the greatest efficiency should logically be preferred, all else equal.
 Inherent risks
are the
risk estimates before accounting for any mitigation efforts. They can
be plotted against a guiding risk response framework where the P-I table
is split covered by overlapping areas of Avoid, Control, Transfer, and
Accept, as shown in the figure on the right.
Inherent risks
are the
risk estimates before accounting for any mitigation efforts. They can
be plotted against a guiding risk response framework where the P-I table
is split covered by overlapping areas of Avoid, Control, Transfer, and
Accept, as shown in the figure on the right.
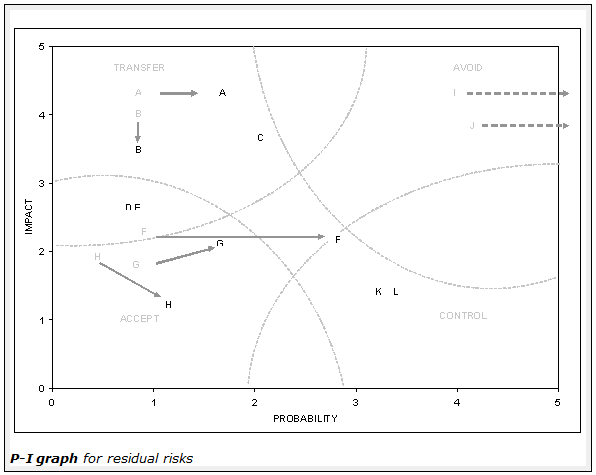
'Avoid' applies where an organization would be accepting a risk without any benefits.
'Control' applies usually to high-probability risks, normally associated with repetitive actions, and are therefore usually managed through better internal processes.
'Transfer' applies to probability, high-impact risks usually managed through insurance or other means of transferring the risk to parties better capable of absorbing the impact.
'Accept' applies for the remaining low probability, low impact risks for which it may not be effective to focus on too much.
The figure below plots residual risks after any implemented risk mitigation strategies and tracks the progress in managing the residual risks compared to the previous year using arrows. Grey letters represent the status of the risk last year if it is different. A dashed arrow pointing out of the graph means that the risk has been avoided. An enhancement to the residual risk graph that you might like to add is to plot each risk as a circle whose radius reflects how comfortable you are in dealing with the residual risk - for example, perhaps you have handled the occurrence of similar risks before and minimised their impact through good management, or perhaps they got out of hand. A small circle represents risks that one is comfortable managing, and large circle the opposite, so the less manageable risks stand out in the plot.
Read on: Planning a risk analysis
Navigation
- Risk management
- Risk management introduction
- What are risks and opportunities?
- Planning a risk analysis
- Clearly stating risk management questions
- Evaluating risk management options
- Introduction to risk analysis
- The quality of a risk analysis
- Using risk analysis to make better decisions
- Explaining a models assumptions
- Statistical descriptions of model outputs
- Simulation Statistical Results
- Preparing a risk analysis report
- Graphical descriptions of model outputs
- Presenting and using results introduction
- Statistical descriptions of model results
- Mean deviation (MD)
- Range
- Semi-variance and semi-standard deviation
- Kurtosis (K)
- Mean
- Skewness (S)
- Conditional mean
- Custom simulation statistics table
- Mode
- Cumulative percentiles
- Median
- Relative positioning of mode median and mean
- Variance
- Standard deviation
- Inter-percentile range
- Normalized measures of spread - the CofV
- Graphical descriptionss of model results
- Showing probability ranges
- Overlaying histogram plots
- Scatter plots
- Effect of varying number of bars
- Sturges rule
- Relationship between cdf and density (histogram) plots
- Difficulty of interpreting the vertical scale
- Stochastic dominance tests
- Risk-return plots
- Second order cumulative probability plot
- Ascending and descending cumulative plots
- Tornado plot
- Box Plot
- Cumulative distribution function (cdf)
- Probability density function (pdf)
- Crude sensitivity analysis for identifying important input distributions
- Pareto Plot
- Trend plot
- Probability mass function (pmf)
- Overlaying cdf plots
- Cumulative Plot
- Simulation data table
- Statistics table
- Histogram Plot
- Spider plot
- Determining the width of histogram bars
- Plotting a variable with discrete and continuous elements
- Smoothing a histogram plot
- Risk analysis modeling techniques
- Monte Carlo simulation
- Monte Carlo simulation introduction
- Monte Carlo simulation in ModelRisk
- Filtering simulation results
- Output/Input Window
- Simulation Progress control
- Running multiple simulations
- Random number generation in ModelRisk
- Random sampling from input distributions
- How many Monte Carlo samples are enough?
- Probability distributions
- Distributions introduction
- Probability calculations in ModelRisk
- Selecting the appropriate distributions for your model
- List of distributions by category
- Distribution functions and the U parameter
- Univariate continuous distributions
- Beta distribution
- Beta Subjective distribution
- Four-parameter Beta distribution
- Bradford distribution
- Burr distribution
- Cauchy distribution
- Chi distribution
- Chi Squared distribution
- Continuous distributions introduction
- Continuous fitted distribution
- Cumulative ascending distribution
- Cumulative descending distribution
- Dagum distribution
- Erlang distribution
- Error distribution
- Error function distribution
- Exponential distribution
- Exponential family of distributions
- Extreme Value Minimum distribution
- Extreme Value Maximum distribution
- F distribution
- Fatigue Life distribution
- Gamma distribution
- Generalized Extreme Value distribution
- Generalized Logistic distribution
- Generalized Trapezoid Uniform (GTU) distribution
- Histogram distribution
- Hyperbolic-Secant distribution
- Inverse Gaussian distribution
- Johnson Bounded distribution
- Johnson Unbounded distribution
- Kernel Continuous Unbounded distribution
- Kumaraswamy distribution
- Kumaraswamy Four-parameter distribution
- Laplace distribution
- Levy distribution
- Lifetime Two-Parameter distribution
- Lifetime Three-Parameter distribution
- Lifetime Exponential distribution
- LogGamma distribution
- Logistic distribution
- LogLaplace distribution
- LogLogistic distribution
- LogLogistic Alternative parameter distribution
- LogNormal distribution
- LogNormal Alternative-parameter distribution
- LogNormal base B distribution
- LogNormal base E distribution
- LogTriangle distribution
- LogUniform distribution
- Noncentral Chi squared distribution
- Noncentral F distribution
- Normal distribution
- Normal distribution with alternative parameters
- Maxwell distribution
- Normal Mix distribution
- Relative distribution
- Ogive distribution
- Pareto (first kind) distribution
- Pareto (second kind) distribution
- Pearson Type 5 distribution
- Pearson Type 6 distribution
- Modified PERT distribution
- PERT distribution
- PERT Alternative-parameter distribution
- Reciprocal distribution
- Rayleigh distribution
- Skew Normal distribution
- Slash distribution
- SplitTriangle distribution
- Student-t distribution
- Three-parameter Student distribution
- Triangle distribution
- Triangle Alternative-parameter distribution
- Uniform distribution
- Weibull distribution
- Weibull Alternative-parameter distribution
- Three-Parameter Weibull distribution
- Univariate discrete distributions
- Discrete distributions introduction
- Bernoulli distribution
- Beta-Binomial distribution
- Beta-Geometric distribution
- Beta-Negative Binomial distribution
- Binomial distribution
- Burnt Finger Poisson distribution
- Delaporte distribution
- Discrete distribution
- Discrete Fitted distribution
- Discrete Uniform distribution
- Geometric distribution
- HypergeoM distribution
- Hypergeometric distribution
- HypergeoD distribution
- Inverse Hypergeometric distribution
- Logarithmic distribution
- Negative Binomial distribution
- Poisson distribution
- Poisson Uniform distribution
- Polya distribution
- Skellam distribution
- Step Uniform distribution
- Zero-modified counting distributions
- More on probability distributions
- Multivariate distributions
- Multivariate distributions introduction
- Dirichlet distribution
- Multinomial distribution
- Multivariate Hypergeometric distribution
- Multivariate Inverse Hypergeometric distribution type2
- Negative Multinomial distribution type 1
- Negative Multinomial distribution type 2
- Multivariate Inverse Hypergeometric distribution type1
- Multivariate Normal distribution
- More on probability distributions
- Approximating one distribution with another
- Approximations to the Inverse Hypergeometric Distribution
- Normal approximation to the Gamma Distribution
- Normal approximation to the Poisson Distribution
- Approximations to the Hypergeometric Distribution
- Stirlings formula for factorials
- Normal approximation to the Beta Distribution
- Approximation of one distribution with another
- Approximations to the Negative Binomial Distribution
- Normal approximation to the Student-t Distribution
- Approximations to the Binomial Distribution
- Normal_approximation_to_the_Binomial_distribution
- Poisson_approximation_to_the_Binomial_distribution
- Normal approximation to the Chi Squared Distribution
- Recursive formulas for discrete distributions
- Normal approximation to the Lognormal Distribution
- Normal approximations to other distributions
- Approximating one distribution with another
- Correlation modeling in risk analysis
- Common mistakes when adapting spreadsheet models for risk analysis
- More advanced risk analysis methods
- SIDs
- Modeling with objects
- ModelRisk database connectivity functions
- PK/PD modeling
- Value of information techniques
- Simulating with ordinary differential equations (ODEs)
- Optimization of stochastic models
- ModelRisk optimization extension introduction
- Optimization Settings
- Defining Simulation Requirements in an Optimization Model
- Defining Decision Constraints in an Optimization Model
- Optimization Progress control
- Defining Targets in an Optimization Model
- Defining Decision Variables in an Optimization Model
- Optimization Results
- Summing random variables
- Aggregate distributions introduction
- Aggregate modeling - Panjer's recursive method
- Adding correlation in aggregate calculations
- Sum of a random number of random variables
- Moments of an aggregate distribution
- Aggregate modeling in ModelRisk
- Aggregate modeling - Fast Fourier Transform (FFT) method
- How many random variables add up to a fixed total
- Aggregate modeling - compound Poisson approximation
- Aggregate modeling - De Pril's recursive method
- Testing and modeling causal relationships
- Stochastic time series
- Time series introduction
- Time series in ModelRisk
- Autoregressive models
- Thiel inequality coefficient
- Effect of an intervention at some uncertain point in time
- Log return of a Time Series
- Markov Chain models
- Seasonal time series
- Bounded random walk
- Time series modeling in finance
- Birth and death models
- Time series models with leading indicators
- Geometric Brownian Motion models
- Time series projection of events occurring randomly in time
- Simulation for six sigma
- ModelRisk's Six Sigma functions
- VoseSixSigmaCp
- VoseSixSigmaCpkLower
- VoseSixSigmaProbDefectShift
- VoseSixSigmaLowerBound
- VoseSixSigmaK
- VoseSixSigmaDefectShiftPPMUpper
- VoseSixSigmaDefectShiftPPMLower
- VoseSixSigmaDefectShiftPPM
- VoseSixSigmaCpm
- VoseSixSigmaSigmaLevel
- VoseSixSigmaCpkUpper
- VoseSixSigmaCpk
- VoseSixSigmaDefectPPM
- VoseSixSigmaProbDefectShiftLower
- VoseSixSigmaProbDefectShiftUpper
- VoseSixSigmaYield
- VoseSixSigmaUpperBound
- VoseSixSigmaZupper
- VoseSixSigmaZmin
- VoseSixSigmaZlower
- Modeling expert opinion
- Modeling expert opinion introduction
- Sources of error in subjective estimation
- Disaggregation
- Distributions used in modeling expert opinion
- A subjective estimate of a discrete quantity
- Incorporating differences in expert opinions
- Modeling opinion of a variable that covers several orders of magnitude
- Maximum entropy
- Probability theory and statistics
- Probability theory and statistics introduction
- Stochastic processes
- Stochastic processes introduction
- Poisson process
- Hypergeometric process
- The hypergeometric process
- Number in a sample with a particular characteristic in a hypergeometric process
- Number of hypergeometric samples to get a specific number of successes
- Number of samples taken to have an observed s in a hypergeometric process
- Estimate of population and sub-population sizes in a hypergeometric process
- The binomial process
- Renewal processes
- Mixture processes
- Martingales
- Estimating model parameters from data
- The basics
- Probability equations
- Probability theorems and useful concepts
- Probability parameters
- Probability rules and diagrams
- The definition of probability
- The basics of probability theory introduction
- Fitting probability models to data
- Fitting time series models to data
- Fitting correlation structures to data
- Fitting in ModelRisk
- Fitting probability distributions to data
- Fitting distributions to data
- Method of Moments (MoM)
- Check the quality of your data
- Kolmogorov-Smirnoff (K-S) Statistic
- Anderson-Darling (A-D) Statistic
- Goodness of fit statistics
- The Chi-Squared Goodness-of-Fit Statistic
- Determining the joint uncertainty distribution for parameters of a distribution
- Using Method of Moments with the Bootstrap
- Maximum Likelihood Estimates (MLEs)
- Fitting a distribution to truncated censored or binned data
- Critical Values and Confidence Intervals for Goodness-of-Fit Statistics
- Matching the properties of the variable and distribution
- Transforming discrete data before performing a parametric distribution fit
- Does a parametric distribution exist that is well known to fit this type of variable?
- Censored data
- Fitting a continuous non-parametric second-order distribution to data
- Goodness of Fit Plots
- Fitting a second order Normal distribution to data
- Using Goodness-of Fit Statistics to optimize Distribution Fitting
- Information criteria - SIC HQIC and AIC
- Fitting a second order parametric distribution to observed data
- Fitting a distribution for a continuous variable
- Does the random variable follow a stochastic process with a well-known model?
- Fitting a distribution for a discrete variable
- Fitting a discrete non-parametric second-order distribution to data
- Fitting a continuous non-parametric first-order distribution to data
- Fitting a first order parametric distribution to observed data
- Fitting a discrete non-parametric first-order distribution to data
- Fitting distributions to data
- Technical subjects
- Comparison of Classical and Bayesian methods
- Comparison of classic and Bayesian estimate of Normal distribution parameters
- Comparison of classic and Bayesian estimate of intensity lambda in a Poisson process
- Comparison of classic and Bayesian estimate of probability p in a binomial process
- Which technique should you use?
- Comparison of classic and Bayesian estimate of mean "time" beta in a Poisson process
- Classical statistics
- Bayesian
- Bootstrap
- The Bootstrap
- Linear regression parametric Bootstrap
- The Jackknife
- Multiple variables Bootstrap Example 2: Difference between two population means
- Linear regression non-parametric Bootstrap
- The parametric Bootstrap
- Bootstrap estimate of prevalence
- Estimating parameters for multiple variables
- Example: Parametric Bootstrap estimate of the mean of a Normal distribution with known standard deviation
- The non-parametric Bootstrap
- Example: Parametric Bootstrap estimate of mean number of calls per hour at a telephone exchange
- The Bootstrap likelihood function for Bayesian inference
- Multiple variables Bootstrap Example 1: Estimate of regression parameters
- Bayesian inference
- Uninformed priors
- Conjugate priors
- Prior distributions
- Bayesian analysis with threshold data
- Bayesian analysis example: gender of a random sample of people
- Informed prior
- Simulating a Bayesian inference calculation
- Hyperparameters
- Hyperparameter example: Micro-fractures on turbine blades
- Constructing a Bayesian inference posterior distribution in Excel
- Bayesian analysis example: Tigers in the jungle
- Markov chain Monte Carlo (MCMC) simulation
- Introduction to Bayesian inference concepts
- Bayesian estimate of the mean of a Normal distribution with known standard deviation
- Bayesian estimate of the mean of a Normal distribution with unknown standard deviation
- Determining prior distributions for correlated parameters
- Improper priors
- The Jacobian transformation
- Subjective prior based on data
- Taylor series approximation to a Bayesian posterior distribution
- Bayesian analysis example: The Monty Hall problem
- Determining prior distributions for uncorrelated parameters
- Subjective priors
- Normal approximation to the Beta posterior distribution
- Bayesian analysis example: identifying a weighted coin
- Bayesian estimate of the standard deviation of a Normal distribution with known mean
- Likelihood functions
- Bayesian estimate of the standard deviation of a Normal distribution with unknown mean
- Determining a prior distribution for a single parameter estimate
- Simulating from a constructed posterior distribution
- Bootstrap
- Comparison of Classical and Bayesian methods
- Analyzing and using data introduction
- Data Object
- Vose probability calculation
- Bayesian model averaging
- Miscellaneous
- Excel and ModelRisk model design and validation techniques
- Using range names for model clarity
- Color coding models for clarity
- Compare with known answers
- Checking units propagate correctly
- Stressing parameter values
- Model Validation and behavior introduction
- Informal auditing
- Analyzing outputs
- View random scenarios on screen and check for credibility
- Split up complex formulas (megaformulas)
- Building models that are efficient
- Comparing predictions against reality
- Numerical integration
- Comparing results of alternative models
- Building models that are easy to check and modify
- Model errors
- Model design introduction
- About array functions in Excel
- Excel and ModelRisk model design and validation techniques
- Monte Carlo simulation
- RISK ANALYSIS SOFTWARE
- Risk analysis software from Vose Software
- ModelRisk - risk modeling in Excel
- ModelRisk functions explained
- VoseCopulaOptimalFit and related functions
- VoseTimeOptimalFit and related functions
- VoseOptimalFit and related functions
- VoseXBounds
- VoseCLTSum
- VoseAggregateMoments
- VoseRawMoments
- VoseSkewness
- VoseMoments
- VoseKurtosis
- VoseAggregatePanjer
- VoseAggregateFFT
- VoseCombined
- VoseCopulaBiGumbel
- VoseCopulaBiClayton
- VoseCopulaBiNormal
- VoseCopulaBiT
- VoseKendallsTau
- VoseRiskEvent
- VoseCopulaBiFrank
- VoseCorrMatrix
- VoseRank
- VoseValidCorrmat
- VoseSpearman
- VoseCopulaData
- VoseCorrMatrixU
- VoseTimeSeasonalGBM
- VoseMarkovSample
- VoseMarkovMatrix
- VoseThielU
- VoseTimeEGARCH
- VoseTimeAPARCH
- VoseTimeARMA
- VoseTimeDeath
- VoseTimeAR1
- VoseTimeAR2
- VoseTimeARCH
- VoseTimeMA2
- VoseTimeGARCH
- VoseTimeGBMJDMR
- VoseTimePriceInflation
- VoseTimeGBMMR
- VoseTimeWageInflation
- VoseTimeLongTermInterestRate
- VoseTimeMA1
- VoseTimeGBM
- VoseTimeGBMJD
- VoseTimeShareYields
- VoseTimeYule
- VoseTimeShortTermInterestRate
- VoseDominance
- VoseLargest
- VoseSmallest
- VoseShift
- VoseStopSum
- VoseEigenValues
- VosePrincipleEsscher
- VoseAggregateMultiFFT
- VosePrincipleEV
- VoseCopulaMultiNormal
- VoseRunoff
- VosePrincipleRA
- VoseSumProduct
- VosePrincipleStdev
- VosePoissonLambda
- VoseBinomialP
- VosePBounds
- VoseAIC
- VoseHQIC
- VoseSIC
- VoseOgive1
- VoseFrequency
- VoseOgive2
- VoseNBootStdev
- VoseNBoot
- VoseSimulate
- VoseNBootPaired
- VoseAggregateMC
- VoseMean
- VoseStDev
- VoseAggregateMultiMoments
- VoseDeduct
- VoseExpression
- VoseLargestSet
- VoseKthSmallest
- VoseSmallestSet
- VoseKthLargest
- VoseNBootCofV
- VoseNBootPercentile
- VoseExtremeRange
- VoseNBootKurt
- VoseCopulaMultiClayton
- VoseNBootMean
- VoseTangentPortfolio
- VoseNBootVariance
- VoseNBootSkewness
- VoseIntegrate
- VoseInterpolate
- VoseCopulaMultiGumbel
- VoseCopulaMultiT
- VoseAggregateMultiMC
- VoseCopulaMultiFrank
- VoseTimeMultiMA1
- VoseTimeMultiMA2
- VoseTimeMultiGBM
- VoseTimeMultBEKK
- VoseAggregateDePril
- VoseTimeMultiAR1
- VoseTimeWilkie
- VoseTimeDividends
- VoseTimeMultiAR2
- VoseRuinFlag
- VoseRuinTime
- VoseDepletionShortfall
- VoseDepletion
- VoseDepletionFlag
- VoseDepletionTime
- VosejProduct
- VoseCholesky
- VoseTimeSimulate
- VoseNBootSeries
- VosejkProduct
- VoseRuinSeverity
- VoseRuin
- VosejkSum
- VoseTimeDividendsA
- VoseRuinNPV
- VoseTruncData
- VoseSample
- VoseIdentity
- VoseCopulaSimulate
- VoseSortA
- VoseFrequencyCumulA
- VoseAggregateDeduct
- VoseMeanExcessP
- VoseProb10
- VoseSpearmanU
- VoseSortD
- VoseFrequencyCumulD
- VoseRuinMaxSeverity
- VoseMeanExcessX
- VoseRawMoment3
- VosejSum
- VoseRawMoment4
- VoseNBootMoments
- VoseVariance
- VoseTimeShortTermInterestRateA
- VoseTimeLongTermInterestRateA
- VoseProb
- VoseDescription
- VoseCofV
- VoseAggregateProduct
- VoseEigenVectors
- VoseTimeWageInflationA
- VoseRawMoment1
- VosejSumInf
- VoseRawMoment2
- VoseShuffle
- VoseRollingStats
- VoseSplice
- VoseTSEmpiricalFit
- VoseTimeShareYieldsA
- VoseParameters
- VoseAggregateTranche
- VoseCovToCorr
- VoseCorrToCov
- VoseLLH
- VoseTimeSMEThreePoint
- VoseDataObject
- VoseCopulaDataSeries
- VoseDataRow
- VoseDataMin
- VoseDataMax
- VoseTimeSME2Perc
- VoseTimeSMEUniform
- VoseTimeSMESaturation
- VoseOutput
- VoseInput
- VoseTimeSMEPoisson
- VoseTimeBMAObject
- VoseBMAObject
- VoseBMAProb10
- VoseBMAProb
- VoseCopulaBMA
- VoseCopulaBMAObject
- VoseTimeEmpiricalFit
- VoseTimeBMA
- VoseBMA
- VoseSimKurtosis
- VoseOptConstraintMin
- VoseSimProbability
- VoseCurrentSample
- VoseCurrentSim
- VoseLibAssumption
- VoseLibReference
- VoseSimMoments
- VoseOptConstraintMax
- VoseSimMean
- VoseOptDecisionContinuous
- VoseOptRequirementEquals
- VoseOptRequirementMax
- VoseOptRequirementMin
- VoseOptTargetMinimize
- VoseOptConstraintEquals
- VoseSimVariance
- VoseSimSkewness
- VoseSimTable
- VoseSimCofV
- VoseSimPercentile
- VoseSimStDev
- VoseOptTargetValue
- VoseOptTargetMaximize
- VoseOptDecisionDiscrete
- VoseSimMSE
- VoseMin
- VoseMin
- VoseOptDecisionList
- VoseOptDecisionBoolean
- VoseOptRequirementBetween
- VoseOptConstraintBetween
- VoseSimMax
- VoseSimSemiVariance
- VoseSimSemiStdev
- VoseSimMeanDeviation
- VoseSimMin
- VoseSimCVARp
- VoseSimCVARx
- VoseSimCorrelation
- VoseSimCorrelationMatrix
- VoseOptConstraintString
- VoseOptCVARx
- VoseOptCVARp
- VoseOptPercentile
- VoseSimValue
- VoseSimStop
- Precision Control Functions
- VoseAggregateDiscrete
- VoseTimeMultiGARCH
- VoseTimeGBMVR
- VoseTimeGBMAJ
- VoseTimeGBMAJVR
- VoseSID
- Generalized Pareto Distribution (GPD)
- Generalized Pareto Distribution (GPD) Equations
- Three-Point Estimate Distribution
- Three-Point Estimate Distribution Equations
- VoseCalibrate
- ModelRisk interfaces
- Integrate
- Data Viewer
- Stochastic Dominance
- Library
- Correlation Matrix
- Portfolio Optimization Model
- Common elements of ModelRisk interfaces
- Risk Event
- Extreme Values
- Select Distribution
- Combined Distribution
- Aggregate Panjer
- Interpolate
- View Function
- Find Function
- Deduct
- Ogive
- AtRISK model converter
- Aggregate Multi FFT
- Stop Sum
- Crystal Ball model converter
- Aggregate Monte Carlo
- Splicing Distributions
- Subject Matter Expert (SME) Time Series Forecasts
- Aggregate Multivariate Monte Carlo
- Ordinary Differential Equation tool
- Aggregate FFT
- More on Conversion
- Multivariate Copula
- Bivariate Copula
- Univariate Time Series
- Modeling expert opinion in ModelRisk
- Multivariate Time Series
- Sum Product
- Aggregate DePril
- Aggregate Discrete
- Expert
- ModelRisk introduction
- Building and running a simple example model
- Distributions in ModelRisk
- List of all ModelRisk functions
- Custom applications and macros
- ModelRisk functions explained
- Tamara - project risk analysis
- Introduction to Tamara project risk analysis software
- Launching Tamara
- Importing a schedule
- Assigning uncertainty to the amount of work in the project
- Assigning uncertainty to productivity levels in the project
- Adding risk events to the project schedule
- Adding cost uncertainty to the project schedule
- Saving the Tamara model
- Running a Monte Carlo simulation in Tamara
- Reviewing the simulation results in Tamara
- Using Tamara results for cost and financial risk analysis
- Creating, updating and distributing a Tamara report
- Tips for creating a schedule model suitable for Monte Carlo simulation
- Random number generator and sampling algorithms used in Tamara
- Probability distributions used in Tamara
- Correlation with project schedule risk analysis
- Pelican - enterprise risk management